파이썬으로 구현한 육각형 기반 시각화 코딩 프로젝트 탐구

1. 서론

컴퓨팅의 발전 속도가 빨라지면서 수집되는 데이터의 양과 종류도 늘어나고 있다. 데이터를 정리하고 원하는 방식으로 변환하는 것은 중요한 역량으로 부각되고 있는데 학교 현장에서 컴퓨팅 사고력의 한 영역으로 차지할 만큼 데이터를 원하는 대로 처리하는 것은 중요한 자산임이 분명하다[1, 14].

하지만 실제 어떻게 그런 역량을 쌓아나갈 수 있는지 그리고 그런 예가 어떤 것인지 보여주기란 쉽지 않다. 데이터 입력에 따라 원하는 출력을 처리하는 컴퓨터 알고리즘을 설계하다 보면 어느덧 데이터를 구체적으로 다루면서 처리할 수 있는 절차(알고리즘)를 구상하게 마련이다[2]. 그런 맥락에서 볼 때 조그만 아이디어에서 출발하여 간단한 데이터를 가지고 여러 가지 방식으로 변환해 보면서 코딩하는 작업이 많은 도움이 된다. 일례로 평면 타일링과 프랙탈 등을 터틀그래픽으로 코딩하면서 자신만의 세계를 구현해 보는 것은 매우 흥미롭고 교육적으로 유용한 활동으로 보고되고 있다[3].

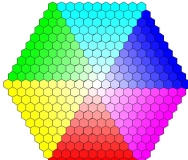
이 논문은 육각형의 픽셀을 자리바꿈하여 데이터를 처리하면서 시각적으로 다양하게 표현해 보자는 동기에서 출발하였다. 이미지를 구성하는 가장 작은 단위인 픽셀은 대다수 정사각형의 형태이다. 기존의 이미지 변환 연산들은 픽셀의 색상 값을 변경하는 방법이 주를 이루며, 색상 값을 유지한 채 위치만을 변경하는 방법도 제시되었다[4].

한편, 기존의 픽셀들은 대다수가 사각형의 형태인데 이를 육각형으로 바꾸면 보다 부드러운 경사 표현이 가능해지는 이점이 있다[5]. 게다가 육각형은 삼각형과 유사하게 3의 배수로 이루어진 데이터를 표현하는 데 유리하다. 일례로, 주역에서 등장하는 육효를 육각형으로 변환하여 다양한 패턴으로 표현한 사례가 이에 해당한다[6, 7]. 그 외에도 자연현상에는 눈의 결정 또는 벌집 모양처럼 육각형으로 평면을 채우는 기하학적 문양이 많이 나타나고 있어 육각형 픽셀을 시각적으로 처리하는 방식은 독자의 많은 관심을 지속해서 끌고 있다.

육각 픽셀의 경우에는 사각 픽셀에서의 좌표계를 그대로 적용하기에 무리가 있기에 별도의 좌표 표기법이 필요하다. 육각 픽셀 좌표계에서의 좌푯값을 구하는 방식과 그렇게 육각 픽셀로 구현된 이미지에서 세 가지 대칭축에 대한 대칭 이동 연산에 따라 이미지 재구성법에 대하여 제안해 본다. 또한 색상 정보를 활용하여 육각 픽셀을 자리바꿈함으로써 다양한 기하학적 문양을 얻을 수 있음을 제시한다.

2. 관련 연구

사각형 또는 육각형을 연속으로 배치하여 평면을 나누거나 평면을 채우는 타일링은 기하 수업 또는 이산수학의 그래프 단원에서 다루는 흥미로운 영역에 해당한다[2]. 초등학교 고학년 학생들도 거북이가 움직이는 거리와 좌우로 회전하는 각도만 알면 정다각형을 반복적으로 그려나갈 수 있기에 패턴에 대한 규칙을 발견하고 반복하여 계산하는 활동을 컴퓨터 코딩의 장점을 살려서 화면에 구현할 수 있다. 이러한 과정에서 컴퓨팅 사고를 함양할 수 있고 창의적인 아이디어를 접목하여 코딩 실력을 확장하게 된다[7, 12].

벌집 모양의 정육각형은 NetLogo와 파이썬에 내장된 터틀그래픽으로 그리는 재미를 느낄 수 있다[3]. 정육각형을 연속으로 배치하여 평면을 구성하는 타일링으로 표현할 수 있고 육각형의 위치를 바꾸어 가면서 배치하여 꽃문양 표현도 가능하다. 이의 응용으로 주역의 6효를 육각형의 연속 배치로 표현하여 응용한 사례를 보면 개개의 육각형과 육각형 클러스터가 이루는 패턴을 중첩하여 보여줌으로써 개별 데이터와 그룹 데이터가 하나의 그물망 속에서 연관되어 표현하는 방식을 얻을 수 있다[6, 7].

이런 일련의 연구는 육각형에 대한 기하 또는 문양적 접근 외에 중첩된 육각형의 배치를 터틀그래픽으로 구현하여 숫자 데이터를 질적으로 표현하는 가능성을 열어주었다. 더 나아가 특정 육각형의 쌍이 서로 자리바꿈을 하였을 때 어떤 모양과 의미가 드러나는지에 대한 추측을 제공해 주었다. 이러한 맥락에서 볼 때 육각 픽셀에 대한 자리바꿈 연산은 더욱 풍부한 육각 이미지 생성을 해 주는 도구가 된다.

한편, 픽셀 변환에 관한 선행 연구를 살펴보면 이주행은 꽃 사진을 찍어서 픽셀을 자리바꿈하는 방식을 Mathematica로 구현하여 추상적인 새로운 이미지를 생성하는 픽셀스택(Pixel Stack)이라는 새로운 개념과 기법을 소개하였다[4]. 그의 방법에 따라 사진의 픽셀에 담긴 색채 정보를 정렬하여 재배치하면 마치 픽셀을 가는 체로 걸어서 무거운 색채 값을 가진 픽셀은 아래로 가라앉는 방식으로 픽셀 이미지를 재배치하여 새로운 이미지를 얻을 수 있게 된다.

학생들은 텍스트로 코딩하고 실행하여 데이터로 보는 결과물보다 이미지 같은 시각적인 결과물을 보는 것이 코딩 학습에 대한 몰입도를 더 높여준다. 시각적인 결과물을 즉각적으로 보면서 원하는 결과가 나오지 않으면 바로 코드에 이상이 있음을 바로 확인할 수 있다[8]. 이러한 시각적 프로젝트는 개발자에게 오류를 수정하면서 코딩 과정을 즐겁게 수행하도록 도와준다.

wing과 ISTE & CSTA, Google은 컴퓨팅 사고력에 대한 구성요소를 아래 Table 1과 같이 정의하고 있다.

Table 1.

Components of Computational Thinking

문제 해결 과정에 대한 대표적인 학자인 Polya(1957)는 문제 해결 단계를 문제 이해, 계획 작성, 계획 실행, 반성의 4단계로 설명하였다[9]. 그리고 유지수(2019)는 문제 해결 과정(최숙영, 2016)에 컴퓨팅 사고력을 적용하여 Table 2와 같이 도식화하였다[10, 11].

Table 2.

Computational thinking elements in problem solving process

육각 조형의 자리 이동 프로젝트의 문제 해결 과정에서 컴퓨팅 사고력을 적용함으로써 컴퓨팅 사고력의 증진을 기대할 수 있다.

3. 육각 조형의 좌표 설계

평면을 빈틈없이 채울 수 있는 다각형은 정삼각형, 정사각형, 정육각형이 있다. 그중 정육각형은 붙여 놓았을 때 서로 많은 변이 맞닿아 있어 구조가 가장 안정적이며 서로 대칭으로 이루고 있다[5]. 육각 픽셀은 이웃한 픽셀과 6방향으로 인접하기에 사각 픽셀의 표현보다 경사면에 있어서 부드러운 표현이 가능하다는 장점이 있다.

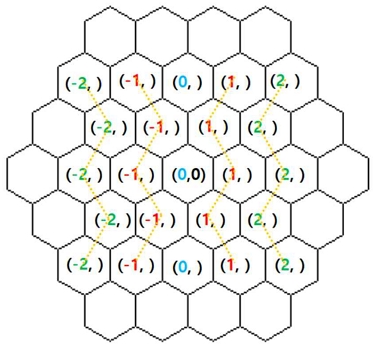
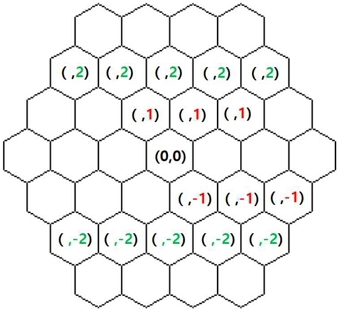
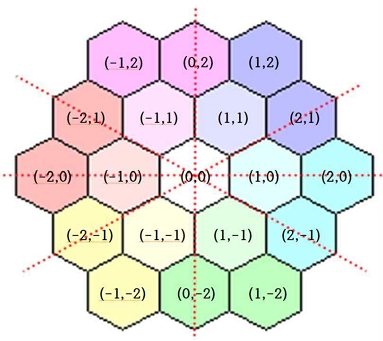
사각형과 달리 육각형의 경우 6방향으로 조형이 배치되기에 이에 대한 좌표 표기법이 필요하다.

Figure 1.

Increase/decrease of X coordinate index value

Figure 2.

Increase/decrease of Y coordinate index value

Figure 3.

(X,Y) coordinate index notation

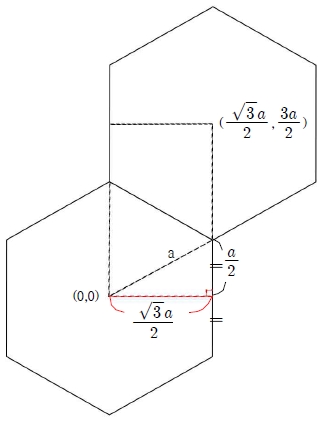
인접 조형 간의 중심 좌푯값은 피타고라스 정리에 따라 구한다.

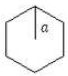
Figure 4는 조형의 크기가 a인 육각 조형에 대하여 원점을 중심으로 인접한 조형 간의 중심 좌표에 대하여 계산한 값이다. 육각형이기에 6방향에 대한 인접한 조형의 중심 좌표를 나열하면 다음과 같다.

Figure 4.

Calculating center coordinate values in hexagonal shape

Y축의 좌푯값은 육각 조형의 크기의 $$ \frac{3}{2}$$배로 하는 규칙을 보이지만 Figure 2를 보면 X축 좌푯값의 경우 Y축 인덱스값이 짝수일 때는 $$ \sqrt{3}a$$배이지만 홀수일 때는 $$ \frac{\sqrt{3}a}{2}$$배인 규칙이 보임을 알 수 있다. 이러한 규칙을 기반으로 좌푯값을 계산하면 된다.

4. 육각 조형의 대칭 이동 연산 구현

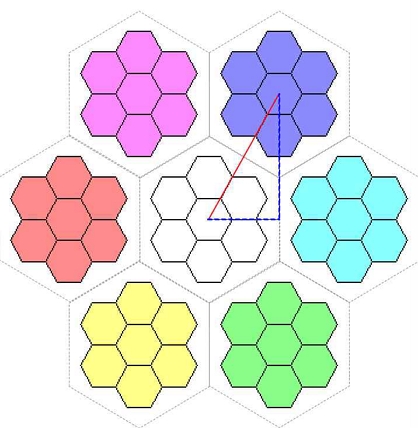
클릭하는 마우스의 좌표에서 가장 가까운 육각 조형을 찾고 해당 육각 조형과 좌표계의 중심을 잇는 선분에 직교하는 직선을 대칭축으로 하는 조형의 위치이동을 수행한다.

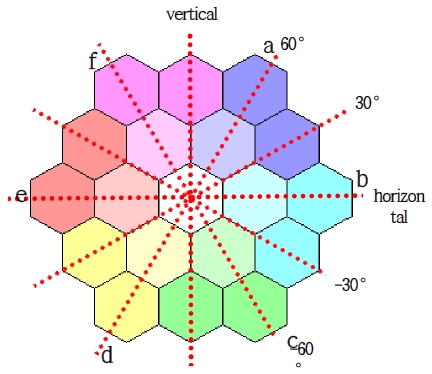
이해를 돕고자 육각형의 각 꼭짓점을 오른쪽 위의 꼭짓점부터 순서대로 a, b, c, d, e, f로 지칭하도록 한다. 대칭 이동의 코드는 크게 대칭축을 결정하기 위하여 마우스로 선택된 방향에 대한 인지 및 대칭축 결정 부분과 대칭 이동 행렬 선택 및 이동된 좌표 계산 부분으로 되어있다.

꼭짓점 a를 클릭하면 direction의 값은 1이고, 꼭짓점 a와 꼭짓점 b 사이의 위치를 클릭하면 direction의 값은 1보다 크고 2보다 작은 값을 갖도록 하였다. 이러한 방식으로 각 꼭짓점과 각 변에 대한 방향에 대한 것을 수치화하면 Table 3과 같다.

Figure 5.

Various axes of symmetry

Table 3.

Axis of symmetry depending on direction

다음은 대칭축에 대한 행렬식을 가져와서 각 조형의 위치에 해당하는 대칭 이동 위치 좌표를 계산하고 화면에 출력하는 코드를 보여준다.

4.1 상하/좌우 대칭

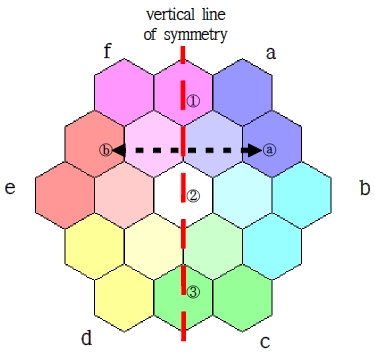
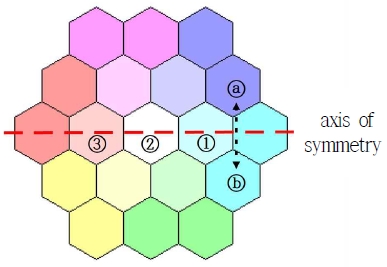
상하 / 좌우 대칭이 되는 경우는 꼭짓점 b와 e 또는 $$ \overline{fa}$$ 또는 $$ \overline{dc}$$를 클릭했을 때 실행된다.

Figure 6.

Swapping along the left and right axis of symmetry

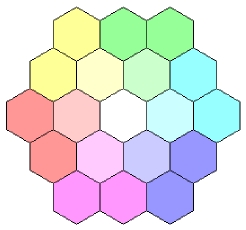
대칭축 선상에 있는 조형들은 위치가 변하지 않기 때문에 조형 ①,②,③은 위치의 변화가 없고, 조형 ⓐ와 ⓑ의 위치를 서로 바꾸는 방식으로 좌우 선대칭 이동을 하게 된다.

좌우 대칭축 행렬은 x=0인 직선에 대한 대칭이기에 다음과 같다.

각 조형의 색상은 유지한 채로 위치만 좌우 대칭이 되도록 변경하는 것이다. 그렇기에 쓰인 색상 값들의 변화 없이 조형의 위치이동을 통해 새로운 이미지를 얻게 된다.

Figure 7.

Image flipped left and right

상하 대칭의 경우도 대칭축 위에 있는 조형 ①,②,③은 위치의 변화가 없고, 조형 ⓐ와 ⓑ의 위치를 서로 바꾸는 방식으로 상하 선대칭 이동을 하게 된다.

Figure 8.

Swapping according to the vertical axis of symmetry

상하 대칭축 행렬은 y=0인 직선에 대한 대칭이기에 다음과 같다.

Figure 9.

Image flipped upside down

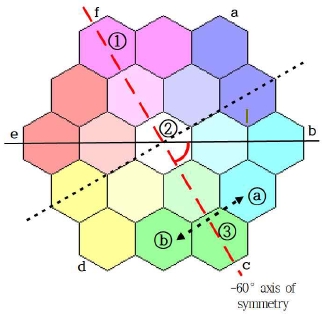
4.2 60° / -60° 대칭

$$ \overline{ab}\left(\overline{ed}\right)$$ 방향 클릭 시 원점에서 $$ \overline{ab}$$으로 내리는 수선은 $$ \overleftrightarrow{l}$$이고 $$ \overleftrightarrow{l}$$와 직교하는 선분인 $$ \overline{fc}$$가 대칭축이 된다.

대칭축 상에 있는 조형 ①,②,③의 위치는 변화가 없고, 조형 ⓐ와 ⓑ의 육각 조형의 위치가 서로 바뀌게 된다.

Figure 10.

Swapping along -60° axis of symmetry

이는 60° 회전하고 x축 대칭 이동한 다음에 다시 –60° 회전한 결과와 같다. 위의 –60° 대칭축에 대한 선대칭 이동 행렬식은 다음과 같이 구하였다.

같은 원리로 $$ \overline{bc}\left(\overline{ef}\right)$$ 방향을 클릭 시 60°인 직선에 대칭이 되도록 육각 조형을 선대칭 이동한다.

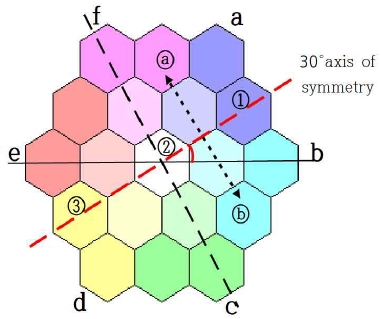
4.3 30° / -30° 대칭

꼭짓점 c(f)에서 원점을 지나는 직선과 직교하는 선분 $$ \overleftrightarrow{l}$$이 대칭축이 된다. 따라서 Figure 11과 같이 기울기가 30°인 직선에 대칭이 되도록 육각 조형이 이동되게 한다.

Figure 11.

Swapping along 30°axis of symmetry

이는 60° 회전하고 y축 대칭 이동한 다음에 다시 –60° 회전한 결과와 같다. 같은 원리로 꼭짓점 a(d)를 클릭 시 -30°인 직선에 대칭이 되도록 육각 조형이 이동되게 한다.

아래는 육각 조형 패턴의 각 대칭축에 대한 이동 예를 정리해 본 표이다.

Table 4.

Swapped hexagon examples along the various axes of symmetry

5. 육각 조형의 클러스터 모형과 응용

조형을 육각형에 그치지 않고 육각형의 군집을 하나의 조형처럼 처리할 수도 있다. 아래 Table 5에 보는 바와 같이 기본 조형이 육각에서 클러스터로 바뀜에 따라 중심 좌표가 육각 조형의 중심에서 클러스터의 중심으로 바뀌게 된다. 그에 따라 육각형 조형의 단위 크기가 바뀌게 된다.

Table 5.

Scaling up with hexagonal clusters

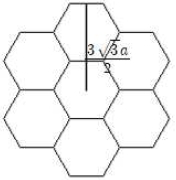
Table 5에서와 같이 30픽셀 크기의 육각 조형과 클러스터의 크기를 비교해 보면 중심에서 외각까지의 길이가 다름을 알 수 있다.

클러스터에서 중심 좌표를 구하는 공식은 기존의 중심 좌표를 구하는 공식에서 기준 길이 a에 대한 값만 바뀌면 되며 기준 길이 a는 다음과 같이 정해지게 된다.

Figure 12.

Calculate the centroid coordinates of a hexagonal cluster

클러스터를 감싸는 육각 조형의 한 변의 길이가 $$ 2\sqrt{3}a$$ 이므로 Figure 4의 a에 $$ 2\sqrt{3}a$$를 대입하면 다음과 같은 중심 좌표들을 얻게 된다.

이는 육각 조형 변의 길이가 $$ 2\sqrt{3}a$$인 경우와 같은 값이다.

아래는 육각형 7개를 하나의 조형처럼 움직이게 하는 예시이다.

Figure 13.

Primary colors of a hexagon cluster

Table 6.

Swapped hexagon clusters along the various axes of symmetry

이렇듯 조형의 도형에 제약을 두지 않기에 보다 다양한 이미지 효과를 얻을 수 있다.

6. 프로젝트에 적용된 컴퓨팅 사고력 요소 분석

문제 인식 단계에서는 육각 조형 이동 프로젝트의 과제가 무엇인지를 파악하는 단계로“기본 도형이 육각형이며 이 육각형이 육각 형태로 반복 배열되고 있고, 색 변화가 있으며, 각 육각형의 위치 이동이 가능한 구조여야 한다.”라고 문제를 분해 및 인지하는 것이다.

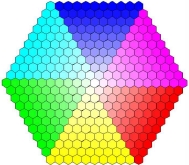
문제 분석 단계는 추상화 단계로 “색상이 중심에서 멀어질수록 채도가 높아지고 연속적인 원형 스펙트럼 형태의 색조 변화, 육각 조형의 배열 형태가 육각형의 형태이다.”라고 정리할 수 있다.

해결 방법 탐색 과정은 문제 해결을 위한 자료의 수집과 분석, 알고리즘 등을 짜는 단계로 “육각형을 그리기 위한 육각형의 기하학적 지식, 색 변화를 주기 위해 컴퓨터상에서의 색상 값 표현하는 방식과 색의 3요소, 터틀 그래픽에서 shape의 사용자 정의 방법” 등 필요한 자료들을 수집하며 “육각 조형 shape 생성 및 육각 배열을 위한 알고리즘 작성” 과정을 수행하게 된다. 즉, 육각 조형들이 자리바꿈하여 재배열되는 규칙성과 각 육각 조형의 중심점 간의 패턴을 찾는 과정들을 거치게 된다.

해결 방법 실천 단계에서는 앞서 작성한 알고리즘들을 기반으로 실제 코딩을 해보고 실행해 보게 된다. 결과물이 이미지의 형태이기에 오류를 직관적으로 인지하게 되며 재수정의 과정을 반복하게 된다.

평가 단계에서 기본 단위인 육각 조형의 변 길이와 전체 layer의 수를 유동적으로 변경할 수 있게 하여 앞의 절차들의 오류가 없는지 검증 평가하는 것이다.

이렇게 육각 조형 이동을 통한 이미지 변환 프로젝트를 진행하는 각 과정에 적용된 컴퓨팅 사고력의 요소들을 정리하면 Table 7과 같이 정리된다.

Table 7

Computational thinking components and examples

앞서 살펴본 바와 같이 향후에 학생들은 이 육각 조형의 자리바꿈 프로젝트를 수행하는 과정에서 컴퓨팅 사고력의 요소들을 경험하게 됨으로써 파이썬 코딩을 통한 컴퓨팅 사고력의 혜택을 얻을 것으로 기대할 수 있다[4, 6, 7, 12].

7. 결론 및 후속 과제

이 연구는 육각 조형의 자리바꿈이라는 아이디어에서 출발하여 다양한 대칭 이동을 통한 이미지를 생성하는 탐구 과정을 제시하였다. 이 연구는 그 사용자가 특정 지점을 클릭하면 그 좌표를 중심으로 육각형의 색채 정보에 따라 정렬되는 방식을 포함하고 있으며 더 나아가 육각형의 꼭짓점을 기준으로 색채 정보에 따라 육각형이 자리바꿈하는 기능도 가지고 있다. 따라서 이 연구에서 제시한 방법은 육각형 조형에서 다양한 방식으로 육각 픽셀을 자리바꿈하는 확장성을 보여주고 있다.

이 연구 결과는 다음과 같은 특징을 보여준다. 첫째, 중심 좌표 계산에서 사용한 피타고라스의 정리는 중학교 2학년 과정에서 나오므로 피타고라스 정리를 선수과정으로 학습한 학생들은 코딩을 통하여 컴퓨팅 사고를 확장할 수 있다. 둘째, 학생들은 육각 조형의 클러스터를 색상 정보 기준으로 볼 때 각각 30°, 60°, 180° 기준으로 대칭 이동할 수 있는 연산을 제시하여 다양한 이미지를 쉽게 얻을 수 있다. 학생들은 육각 조형의 색감을 바꾸는 활동을 통해 미적인 흥미를 느끼면서 오류 발생 시 직관적으로 쉽게 파악할 수 있다.

이 연구에 참여한 제1 저자는 육각형 모양을 중첩하여 표현하는 일종의 데이터 시각화 코딩 작업을 하면서 육각형 클러스터의 대칭 이동에 대한 패턴을 인식하고 파이썬 코딩으로 구현함으로써 코딩 능력의 향상뿐만 아니라 컴퓨팅 사고가 확장됨을 보여주었다[12]. 파이썬으로 데이터를 시각화하는 이러한 코딩 활동은 초등학생들에게 컴퓨팅 사고력을 증진한다는 연구 결과를 참고할 때 고등학생 이상의 학생들과 예비 교사들에게도 적용될 수 있는 여지가 많다[1, 14].

전반적으로 볼 때 이러한 사례는 프로젝트 처리 또는 문제 해결에서 원하는 결과를 얻기 위하여 알고리즘을 설계하고 데이터 조작과 변환을 통해 원하는 결과를 코딩으로 완성하는 작업이 곧 알고리즘의 구현이 됨을 체험하는 측면에서 볼 때 컴퓨터 교육의 핵심이 된다고 볼 수 있다. 비슷한 맥락에서 전영국(2018)은 사다리 게임을 대상으로 123 -> 321처럼 거꾸로 된 순열에 해당하는 사다리의 종류를 Mathematica 코딩으로 생성하여 최소 생성 사다리의 특성을 조사한 바가 있다[15]. 또한 Mathematica를 사용하여 이산구조를 시각적으로 보여주는 코딩 작업은 상호연결통신망을 생성하는 영역[16]에서와 같이 컴퓨팅 사고를 확대할 수 있음을 보여주었다. 본 연구에서 제시한 육각형 기반의 조형 패턴에 대한 시각화 작업도 창의적인 문양을 생성하는 데 유용하게 활용될 수 있으며 그 과정에서 컴퓨팅 사고력을 함양하는 결과를 기대할 수 있다.

전반적으로 볼 때 이 연구의 결과는 파이썬을 활용하여 육각 문양의 픽셀을 자리바꿈하여 다양한 디자인 아이디어를 얻을 수 있는 토대를 마련해 주었다[3, 13]. 앞으로 풍경 사진과 같은 이미지에 대하여 육각 픽셀을 적용 후에 특정 픽셀의 쌍을 서로 자리바꿈해 보면 이주행의 픽셀 스왑과 다른 새로운 이미지를 얻을 수 있다[4]. 또한 육각형의 클러스터를 이용하여 주역의 6효[6, 7]에 해당하는 의미를 시각적 정보와 색채의 조합적 구조로 변형하여 새로운 이미지를 생성해 볼 수 있는 새로운 접근법을 제시해 주었다. 또한 2022년 개정 교육과정에서 강조된 바와 같이 이 논문에서 제시하는 프로젝트가 앞으로 정보 교과 및 방과 후 코딩 수업에서 활용되면 컴퓨팅 사고력(Table 2 참고)을 함양하는 데 이바지할 것으로 판단 된다.

Acknowledgments

본 논문은 2024년 동계 학술대회에서 “육각픽셀을 이용한 이미지 변환”의 제목으로 발표된 논문을 확장한 것임.

References

• Kim, Y., & Kim, J. (2017). Effect of data visualization using Scratch on improvement of creativity of preliminary coding instructors. Journal of The Korean Association of Information Education, 21(3), 309-320. [https://doi.org/10.14352/jkaie.2017.21.3.309]
• Jun, Y., & Yoon, J. (2016). Case exploration of a gifted student’s spontaneous and creative project activities using NetLogo in a math-information combined class. Journal of Science Education for the Gifted, 8(3), 145-166.
• Kim, Y., & Jun, Y. (2022). Exploring Python coding practices of traditional patterns. Proceedings of the Korean Association of Information Education, 26(1), 139-141.
• Lee, J-H. (2019). Image transformation based on positional rearrangement of pixels. Proceedings of the Korea HCI, 87-90
• Kim, H. (2015). A study on the ceramic dessert ware design through repetition and variation of the hexagonal unit form. Master thesis at Seoul National University of Science and Technology.
• Shin, S., & Jun, Y. (2023). Exploring the visualization of ‘I Ching’ patterns using Python. Proceedings of the Korean Association of Information Education, 27(1), 103-106.
• Shin, S. (2023). Exploring visualization of hexagonal patterns based on the I Ching. Master thesis at Suchon National University
• Lee, J-H. (2020. 10). Painting created out of codes: a computer scientist tells a story of artificial intelligence and art. Daejeon Biennale 2020 AI, 106-115.
• Polya, G. (1957) How to Solve It. A New Aspect of Mathematical Method. 2nd Edition, Princeton University Press, Princeton.
• Choi, S. (2016). A Study on Teaching-learning for Enhancing Computational Thinking Skill in terms of Problem Solving. The Journal of Korean Association of Computer Education, 19(1), 53-62.
• Yoo, J.,(2019). Development and Application of Evaluation Items of Computational Thinking based on Problem-Solving Skills for Elementary School Students. Master thesis at Seoul National University of Education
• Jun, Y. (2015). A qualitative case study of computer programming and unfolding creative processes: focusing on NetLogo-based computational thinking. Journal of Korean Association of Computer Education, 18(3), 1-14. http://www.riss.kr/link?id=A100525600
• Lee, S-R. (2008). Analysis of patterns of Korean traditional window grille in point of computer graphics. Journal of KIIT, 6(5), 115-121.
• Lee, J. (2021). Effects of data visualization education using Python on improvement of computational thinking ability in information gifted students of elementary school. Master thesis at Korea National University of Education.
• Jun, Y. (2018). Implementation of an algorithm that generates minimal spanning ladders and exploration on its relevance with computational thinking. Journal of Korean Association of Computer Education, 21(6), 39-47. [https://doi.org/10.32431/kace.2018.21.6.004]
• Seong, B., & Jun, Y. (2022). Mathematica-based visualization analysis for interconnection networks of NSEP Graph and Circle Graph. Journal of Field-based Lesson Studies, 3(2), 89-108. [https://doi.org//10.22768/JFLS.2022.3.2.89]