
강제배분 상대평가를 위한 시험문항 배점 조정 연구
초록
대학에서 학업 성적을 평가하여 등급을 부여하는 방법 중에서 학점별 비율에 대한 규칙을 적용하는 강제배분 상대평가의 경우에는 평가에서 얻어진 점수와 그 점수의 집단 내 상대적인 위치가 학점의 중요한 변수로 작용한다. 특히 많은 수의 분반이 개설되는 교양 필수 과목의 경우에는 동일 교수자가 여러 분반을 맡아서 같은 학습 내용과 평가로 수업을 진행하기도 한다. 이런 경우 분반별로 강제배분 상대평가를 함으로 인해서 동일 교수자의 평가에서 동일 점수를 받은 학생들이 각 그룹에서 서로 다른 등급을 받을 수도 있다. 또한 높은 점수를 받은 학생이 낮은 점수를 받은 학생보다 더 아래 등급을 받는 경우도 발생할 수 있으며, 이는 수업후에 가지는 학생들의 성취감 효과에 영향을 줄 수 있다. 이에 본 논문에서는 모든 그룹의 평균이 목표평균에 근접하고, 각 그룹에서 학점별 비율이 바뀌는 구간의 점수 차이를 최소화할 수 있는 시험 문항 배점 조정 알고리즘을 제시한다. 제시한 알고리즘을 기존의 성적처리에서 실험해 본 결과 그 효과를 확인할 수 있었다.
Abstract
In the case of forced distribution relative evaluation, which applies rules on the ratio of each credit among the methods of evaluating academic performance and assigning grades in universities, the score obtained from the evaluation and the relative position of that score within the group act as important variables of the grade. In particular, in the case of liberal arts required courses where a large number of classes are opened, the same professor may teach several classes with the same learning content and evaluation. In such cases, students who received the same score in the evaluation by the same professor may receive different grades in each group due to forced distribution relative evaluation by class. In addition, there may be cases where students with high scores receive lower grades than students with low scores, which may affect the sense of accomplishment students have after class. In this paper, we propose an algorithm for adjusting the weighting of test items that the average of all groups approaches the target average and can minimize the difference in scores in the section where the ratio of each credit changes in each group. The effectiveness of the proposed algorithm was confirmed by testing it in the existing grade processing.
Keywords:
programming education, difficulty adjustment, relative evaluation, same weighting of items, differential weighting of items키워드:
프로그래밍 교육, 난이도 조정, 상대평가, 동일 배점, 차등 배점1. 서론
대학에서 학업 성적을 평가하여 등급을 부여하는 방법 중에는 절대평가와 상대평가가 있다. 절대평가는 미리 절대 기준을 정해두고 이 기준에 어느 정도 도달하였는지를 평가하는, 즉 수업 목표의 달성도를 평가하는 방법으로 정해진 기준에 따라 등급을 매기는 방법이고, 상대평가는 수업 목표의 달성도를 직접적으로 측정하기보다는 특정 집단 안에서 학생들의 성적이 정규분포를 이룰 것이라는 가정하에 각 학생의 상대적 위치를 판정하고 일정 비율에 따라 등급을 매기는 방법이다. 절대평가에서는 교수자가 수업 목표를 정하고, 그 목표에 도달할 수 있는 수업 내용과 평가 항목 그리고 절대 기준을 정하는 고유 권한을 가질 수 있고, 학생들도 같은 그룹 내 다른 학생들의 학업 능력에 상관없이 자신의 학습 목표에만 집중할 수 있다는 장점이 있다. 하지만 교수자 간에 성적 등급에 대한 절대 기준이 서로 다를 수 있고, 교과목 또는 학과, 계열 간에 성적 등급 분포의 불균형을 초래할 수 있다. 반면 상대평가는 절대평가보다 학습한 전체 학생들의 등급이 한쪽으로 몰리는 것을 예방할 수 있고, 이 방법을 적절히 이용하면 학생들의 학습 동기를 유발할 수 있는 장점이 있다. 하지만 집단 내의 상대적인 위치로 평가한 등급은 집단이 다를 경우에는 해당 등급이 어느 정도의 학업 성취도를 이루었는지 비교하는 것이 어려울 수도 있다.
대학에서 학생들의 학업 성취도를 파악하는 데 주로 시험을 사용하며, 시험에서 얻어진 점수로 등급 부여의 기준으로 삼는다. 일반적으로 시험점수는 시험을 구성하고 있는 여러 개의 문항 점수에서 얻어지는 점수를 합산하는 방식으로 산정된다. 이러한 시험점수를 위하여 각 문항에 점수를 부여하는 방법은 동일 배점과 차등 배점이 있다. 동일 배점은 문항 점수를 부여할 때 각 문항에 같은 가중치를 주는 방법이다. 이는 문항 내용의 중요도와 난이도 등의 문항 간 특성을 고려하지 않는 경우에 일반적으로 사용되며, 점수 가지수가 최대 '문항수+1'로 제한되는 특징이 있다. 차등 배점은 문항 점수를 부여하는 데 문항에 따라 서로 다른 가중치를 주는 방법이다. 이는 문항들의 중요도와 난이도 등으로 일정한 기준을 정하고, 그 기준에 근거하여 시험에서 개별 문항의 비중을 달리하여 문항 점수를 부여한다. 이러한 차등 배점은 학생들이 받을 수 있는 원점수의 가지수를 증대시킬 수 있기 때문에 상대평가에서 더 효율적일 수 있다.
본 논문에서는 대학에 많은 수의 분반이 개설되는 교양 필수 과목에 대하여, 동일 교수자가 여러 분반을 맡아서 같은 학습 내용으로 수업을 진행하고 같은 시험 문항으로 평가를 수행하여 분반별 강제배분 상대평가로 학점을 부여하는 것에 초점을 맞추고자 한다. 일반적으로 교수자는 분반의 학습 능력을 예측하고 시험 결과에 대한 목표평균 점수를 정하여, 문항의 유형이나 난이도 등을 스스로 판단하여 시험 문제를 낸다. 하지만 다양한 학과와 학년으로 구성된 각 그룹의 학습 능력은 교수자의 판단과는 다를 수 있기에 평가 결과도 다양하게 나올 수 있다. 그 결과 분반별 강제배분 상대평가를 했을 때 학습 능력이 서로 다른 분반에서 동일 위치에 있는 학생들의 점수 차이가 크게 날 수도 있다. 예를 들어 분반(A)에서 상위 30% 위치의 점수가 85점이지만 분반(B)의 상위 30% 위치의 점수는 70점일 수 있으며, 이 경우 분반별 강제배분 상대평가에서는 같은 등급이 부여될 수 있다. 또한 분반(A)에서 더 높은 점수를 받은 학생이 분반(B)에서 더 낮은 점수를 받은 학생보다 아래 등급을 받을 수도 있다. 이는 특정 학생이 속한 그룹에서의 학습 능력에 대한 순위로 등급이 결정되는 것이므로 공정성을 훼손했다고 볼 수는 없다. 하지만 수업이 끝난 후에 학생들이 무언가를 배우고 이루었다는 성취감과 자신감을 가지는 측면에서 봤을 때, 낮은 점수로 높은 등급을 받은 학생들에게는 효과가 클 수 있지만 높은 점수로 낮은 등급을 받은 학생들에게는 오히려 그 효과를 감소시키는 이유가 될 수 있다. 이에 본 논문에서는 분반별 강제배분 상대평가를 위하여 모든 분반의 평균이 목표평균에 근접하고, 서로 다른 분반에서 같은 등급을 받은 학생들의 점수 차이를 최소화할 수 있는 문항의 차등배점 조정 알고리즘을 제시한다.
논문의 구성은 다음과 같다. 2장에서는 강제배분 상대평가에 관련된 연구들과 동일 배점과 차등 배점에 관한 연구들을 살펴본다. 3장에서 본 논문에서 제시하는 강제배분 상대평가를 위한 그룹별 배점 기준과 이를 기준으로 한 문항의 차등 배점 조정 알고리즘을 설명한다. 4장에서는 논문에서 제시하는 알고리즘을 실제 평가 결과에서 실험하여 결과를 비교 분석한다. 마지막으로 5장에서 결론과 향후 연구계획을 설명한다.
2. 관련 연구
강제배분 상대평가는 구성원들의 성과를 평가할 때 절대적 기준에 의해 등급을 부여하지 않고, 구성원들의 성과를 서로 비교하여 미리 설정된 비율로 평가 등급을 부여하는 방식이다. 이러한 방식이 예상할 수 있는 긍정적 효과 때문에 기업 현장에서 많이 활용됐음에도 불구하고 그것의 실제 효과나 세부 메커니즘에 관한 연구는 그리 많지 않다. 강제배분 상대평가 제도가 성과에 미치는 효과를 검증한 연구에는 절대평가 제도와 강제배분 상대평가 제도하에서 성과가 어떻게 변하는지, 평가자들이 강제배분 상대평가 제도하에서 평가하는 것이 얼마나 어려운지, 성과를 평가한 관련 연구에서 상대평가에 관한 연구가 차지하는 비중이 4%에도 미치지 못한다는 것을 입증한 연구 등이 대표적이다[1-4]. 따라서 많은 연구자들은 실제와 학문 간의 차이를 줄이기 위해서 강제배분 상대평가 제도에 관한 연구가 더욱더 활성화되어야 한다고 제안하고 있다[5-7].
다음으로 평가를 위한 문항 배점에 있어 동일 배점과 차등 배점의 장단점을 연구한 이전 연구들이 많이 있다. [8, 9]의 연구에서 차등 배점의 효과를 분석한 결과 수험자들을 줄세울 필요가 없는 자격 부여 또는 선발시험의 경우에는 차등 배점보다는 동일 배점을 적용하는 것이 더 적절하며, 수험자들을 줄 세워서 상대평가를 해야 하는 시험의 경우에는 일정한 검사 양호도를 확보하면서도 관찰된 검사 점수의 수가 동등 배점 수보다 2배 이상 증가하여 동점자 해소의 효과가 있는 차등 배점이 더 효율적일 수 있다고 설명하고 있다. 특히 [8]의 연구에서는 차등 배점의 경우에 평가 그룹의 학습 능력과 상관없이 항상 어려운 문항에 높은 점수를 부여하는 것이 타당하다고 볼 수는 없으며, 어떤 기준을 적용할 것인가는 합의와 의사결정의 문제라고 설명하고 있다. 또한 문항 배점을 결정하는 기준은 언제나 명료해야 하며 해당 검사의 모든 문항에 일관되게 적용되어야 함을 강조하고 있다. [9]의 연구에서는 차등 배점 적용 때 최소배점과 최대배점 간의 차이가 3배 미만으로 설정해야 함을 강조하였다. 이는 문항의 구조나 형태가 같을 때는 그 가치가 3배 이상이라고 보기 어려우며, 3배 미만으로 설정하여도 동점자를 해소하기에 필요한 점수 가지수 증대는 충분히 가능하기 때문에 무리하게 문항 간 점수 차이를 3배 이상으로 할 필요가 없음을 시사하고 있다. [10]의 연구에서는 특정 문항의 외형적 형태가 학습 능력이 낮은 시험자의 응답 동기를 저하시켜 문항 응답률을 감소시킴으로써 결과적으로 검사의 정확성을 저하하는 상황이 유발될 가능성을 설명하고 있으며, 이는 시험 문항의 형태를 결정할 때 집단의 학습 능력을 함께 고려하는 것이 시험자의 능력 추정의 정확도를 높이는 방안이 될 수 있음을 시사하고 있다.
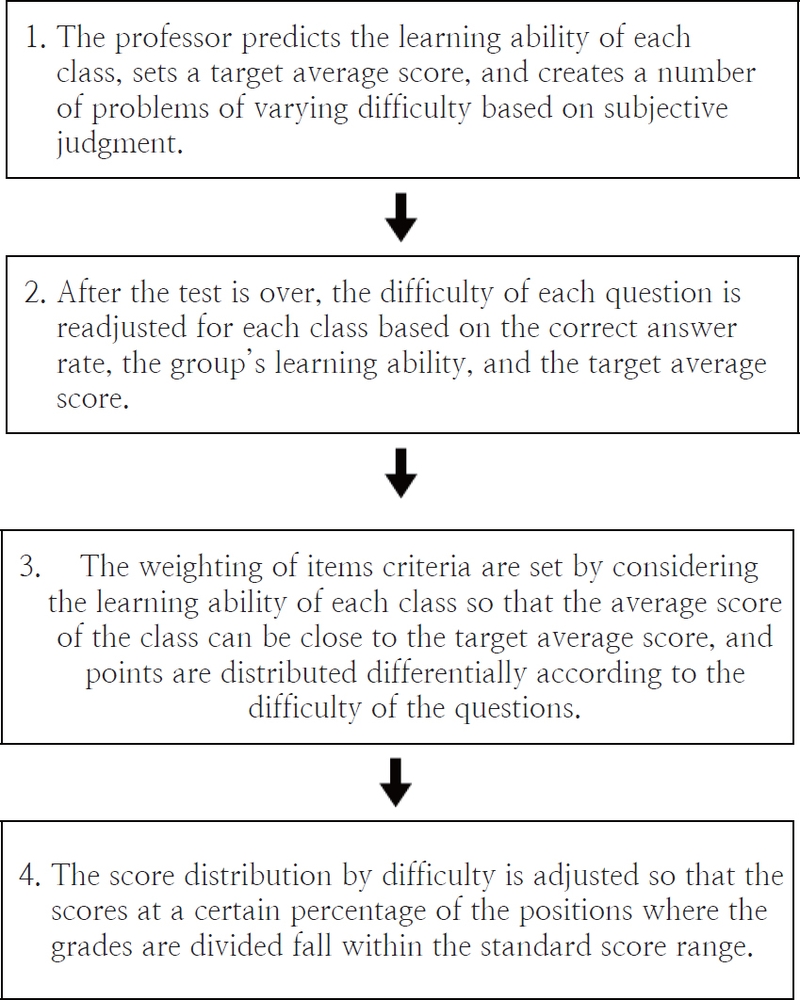
본 논문에서는 이러한 이전 연구들의 근거를 기반으로 분반별 강제배분 상대평가를 위하여 시험에 응시한 모든 분반의 그룹평균이 목표평균에 근접할 수 있는 배점 기준을 적용하고, 등급이 나뉘는 일정 비율 위치의 분반별 점수 차이를 최소화할 수 있도록 문항의 차등배점을 조정하는 알고리즘을 제시한다. Fig. 1에서 전체 알고리즘의 개략적인 과정을 설명한다. 첫째 교수자는 분반의 학습 능력을 예측하여 목표평균 점수를 정하고, 주관적인 판단으로 난이도별 문제수를 출제한다. 이때 문항의 최대배점과 최소배점을 정하고, 개별 문항에 대한 배점은 정하지 않는다. 둘째 시험이 끝난 후에 문항의 정답률과 그룹의 학습 능력 그리고 목표평균 점수를 이용하여 분반별로 각 문항의 난이도를 재조정한다. 셋째, 분반의 그룹평균 점수가 목표평균 점수에 근접할 수 있도록 차등 배점 기준을 정하고, 문항 난이도별로 차등 배점하여 성적처리를 수행한다. 넷째, 등급이 나뉘는 일정 비율 위치의 점수가 기준점수 범위에 들어올 때까지 난이도별 차등 배점을 조정한다.
3. 강제배분 상대평가를 위한 문항의 차등 배점 조정 알고리즘
3.1 난이도와 유형을 고려한 문제 출제
최초 교수자는 주관적인 판단에 따라 그룹의 학습 능력을 예측하여 목표평균 점수를 정하고, 이를 위한 시험 문항의 난이도별 개수를 정하여 출제한다. 각 난이도별 문제수 비율은 [11, 12]의 연구에서 제시한 알고리즘을 기반으로 한다. [11]의 연구에서 문제 출제 시 출제된 전체 문제들의 정답률 평균이 예상 평균 점수가 되도록 난이도별 문제수 비율을 제시하였다. 이때의 예상 평균 점수는 모든 문항에 동일 배점을 적용하여 계산한 결과이다. Table 1은 이 연구에서 구한 예상되는 평균 점수에 따른 문제수 비율이다. 예를 들어 목표평균 점수를 70점으로 정하고 총 25개의 시험 문제를 낸다고 했을 때, 출제되는 난이도별 문항의 개수는 상(upper) 0개(0%), 상중(upper-middle) 2개(7%), 중(middle) 6개(24%), 중하(middle-low) 10개(42%), 하(low) 7개(27%)이다.
[12]의 연구에서는 프로그래밍 언어의 특성을 고려하여 객관식 문제를 유형1(문법)과 유형2(알고리즘)로 구분하였다. 같은 난이도'상'문제인 경우에 학습자들은 유형2 문제를 더 어려운 문제라고 생각하고, 같은 난이도'하'인 경우에 학습자들은 유형1 문제를 더 쉬운 문제라고 생각한다는 실험 결과를 토대로, 문제의 난이도와 유형을 함께 고려하여 난이도별 문제수를 출제하였다. 본 논문에서는 이 연구에 근거하여 난이도별 개수가 홀수일 때, 난도가 높은 문제에서는 유형2(type2)를 더 출제하고 난이도가 쉬운 문제에서는 유형1(type1)을 더 출제한다.
Table 2는 목표평균 60점과 70점에 대하여 총 25개의 시험 문제를 낼 때의 난이도와 유형에 따른 출제 문제수이다. Table 2를 기준으로 출제한 문제로 평가를 한 후에 모든 문항의 정답률과 동일 배점을 적용한 그룹평균을 계산한다.
3.2 문항별 난이도 재조정
교수자는 그룹의 학습 능력이 정규분포를 이룰 것으로 예측하고 목표평균을 정하여 난이도별 문항 개수를 정하지만, 교수자의 예측과는 달리 모든 그룹의 학습 능력이 정규분포를 이루고 있다고 가정하기는 어렵다. 또한 교수자가 결정한 특정 문항의 난이도는 시험에 응시한 개인 또는 그룹들의 학습 능력에 따라 쉽고 어려움의 정도가 매우 다를 수 있다. 실제로 목표평균을 위해서는 학습 능력이 높은 그룹에는 난이도가 어려운 문제를 더 많이 출제해야 하고, 학습 능력이 낮은 그룹에는 난이도가 쉬운 문제를 더 많이 출제해야 한다. 이에 난이도별 차등 배점을 위해 시험 응시 후에 그룹별로 학습 능력에 따라 시험 문항의 난이도를 재조정한다. 즉 그룹의 학습 능력에 따라서 전체 문항의 난이도의 개수가 달라진다.
예를 들어 학습 능력이 높은 그룹에서 많이 틀린 문제는 학습 능력이 낮은 그룹에서 많이 틀린 문제보다는 상대적으로 난이도를 더 높게 측정한다. 반대로 학습 능력이 낮은 그룹에서 많이 맞춘 문제는 학습 능력이 높은 그룹에서 많이 맞춘 문제보다는 난이도를 더 낮게 측정한다. 따라서 문항의 정답률과 그룹평균 그리고 교수자가 정한 목표평균 점수를 이용하여 각 문항의 난이도 비율을 다음으로 계산한다.
계산된 난이도 비율에 따라 각 문항의 난이도는 Table 3과 같이 5개로 세분화된다.
각 그룹에서 특정 문항의 난이도 비율 계산과 그에 따라 결정된 난이도를 살펴보자. 예를 들어 그룹의 목표평균이 70점인 시험 문제를 A/B/C 3개의 그룹에서 치른 후에 각 문항에 동일 배점을 적용하여 그룹별 평균을 구한 결과, 그룹(A)의 그룹평균이 85점, 그룹(B)의 그룹평균이 72점, 그룹(C)의 그룹평균이 55점이라고 가정해 보자. 이때 정답률이 73%인 특정 문항의 난이도 비율을 A/B/C 3개의 그룹에서 계산하면 다음과 같다.
이는 정답률이 높은 문항의 경우에 상대적으로 학습 능력이 더 낮은 그룹에서 많이 맞춘 경우가 학습 능력이 높은 그룹에서 많이 맞춘 경우보다는 더 쉬운 문제로 간주되어 난이도가 결정된다.
다음 예로 정답률이 35%인 특정 문항의 난이도 비율을 그룹평균이 85점인 그룹(A), 그룹평균이 72점인 그룹(B), 그룹평균이 55점인 그룹(C)에서 계산하면 다음과 같다.
이는 정답률이 낮은 문항의 경우에 상대적으로 학습 능력이 더 높은 그룹에서 많이 틀린 경우가 학습 능력이 낮은 그룹에서 많이 틀린 경우보다는 더 어려운 문제로 간주되어 난이도가 결정된다.
3.3 목표평균을 위한 차등 배점 기준 설정
일반적으로 시험 문항에 차등 배점을 적용할 때 어려운 문항에 높은 배점을 적용하고, 쉬운 문항에 낮은 배점을 적용하는 방식을 많이 사용한다. 따라서 대부분 응시자의 전체 맞힌 문항 중에는 어려운 문항보다는 쉬운 문항이 더 많으므로 동일 배점을 적용했을 때의 그룹평균에 비해 차등 배점을 적용했을 때의 그룹평균이 더 낮아지는 현상이 발생한다. Table 4 는 7개 그룹의 시험 결과에서 동일 배점과 차등 배점을 적용했을 때의 그룹평균을 비교한 예시이다. 이때의 차등 배점은 모든 그룹에 같은 기준으로 어려운 문항에 높은 배점을, 쉬운 문항에 낮은 배점을 적용하였다.
Table 4의 결과는 예상 평균 점수 70을 기준으로 난이도별 문제수를 정하여 25개의 문제를 출제하였다. 동일 배점은 모든 문항 점수를 4점으로 계산한 결과이다. 차등 배점은 교수자의 판단을 배제하고 정답률 순위만으로 상중(2개), 중(6개), 중하(10개), 하(7개)로 구분하고, 배점은 상중(6점), 중(5점), 중하(4점), 하(2.5점)로 계산하였다. 결과에서 보이듯이 모든 그룹평균이 동일 배점에 비해 차등 배점에서 더 낮아지는 것을 확인할 수 있다. 그 결과 학습 능력이 높은 그룹은 동일 배점보다 차등 배점을 적용했을 때 목표평균 70점에 가까워지는 효과가 있지만, 학습 능력이 낮은 그룹의 경우에는 목표평균 70점에서 더 멀어지는 현상이 발생한다.
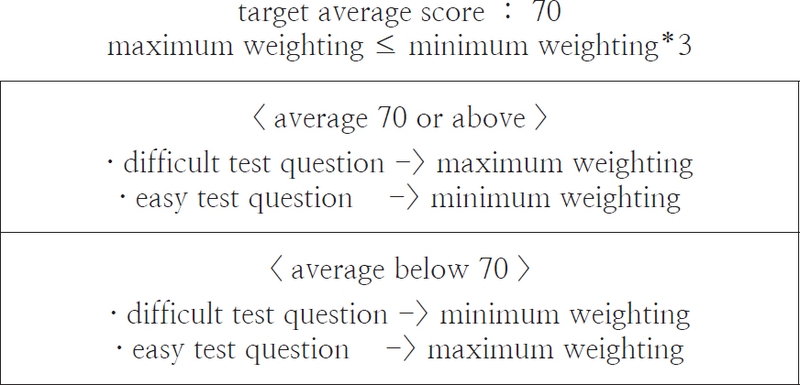
이에 본 논문에서는 [8]의 연구를 근거로 모든 그룹의 그룹평균이 목표평균 점수에 근접할 수 있도록 그룹별로 학습 능력에 따라서 문항의 차등 배점 기준을 달리 정한다. 3.2에서 설명했듯이 그룹의 목표평균을 위해서 학습 능력이 높은 그룹에서는 어려운 문항의 비중을 늘리고, 학습 능력이 낮은 그룹에서는 쉬운 문항의 비중을 늘리기 위함이다. Fig. 2에서 이를 설명하고 있다. 시험 응시 전에는 [9]의 연구를 근거로 최소배점과 최대배점의 차이를 3배 이하 즉, [최대배점 ≤ 최소배점*3]이 되도록 값을 정한다. 그리고 시험 응시 후에 그룹의 학습 능력에 따라서 분반별로 최소배점과 최대배점을 적용할 기준을 설정한다. 먼저 그룹의 학습 능력이 높은 경우 즉, 동일 배점을 적용했을 때의 그룹평균이 목표평균에 비해 높은 경우에는 어려운 문항에 최대배점을 설정하고, 쉬운 문항에 최소배점을 설정한다. 이는 어려운 문항의 비중을 늘림으로써 전체 그룹의 평균 점수를 낮추는 효과를 가져올 수 있다. 다음으로 그룹의 학습 능력이 낮은 경우 즉, 동일 배점을 적용했을 때의 그룹평균이 목표평균에 비해 낮은 경우에는 쉬운 문항에 최대배점을 설정하고, 어려운 문항에 최소배점을 설정한다. 그 결과 쉬운 문항의 점수 비중이 늘어나면서 전체 그룹의 평균 점수를 높이는 효과를 가져올 수 있다.
3.4 학점별 비율이 나뉘는 구간의 기준점수를 위한 배점 조정
일반적으로 대학에서 상대평가로 학점을 부여할 때 학점별 비율에 관한 규정이 존재한다. 예를 들어 A+/A0 학점은 0~30%, B+/B0 학점은 30~70%, C+/C0/D+/D0/F 학점은 30~60%인 경우이다. 이는 A+/A0 학점은 최대 30%까지 학점 부여가 가능하다는 의미이고, C+ 이하 학점 비율은 최소 30% 이상 부여해야 한다는 의미이다. 시험 결과에서 학생들은 자신이 속한 그룹의 성적 순위 30% 또는 70% 위치의 점수와 자신의 점수를 비교하여 자신이 받을 수 있는 학점 범위를 예측할 수 있다. 이에 본 논문에서는 등급이 나뉘는 일정 비율 위치의 그룹별 점수 차이를 최소화할 수 있도록 난이도별 배점을 재조정한다. 먼저 3.3의 차등 배점 기준에 따라 전체 100% 비율에 맞추어 난이도별 배점을 정하여 성적처리를 수행한다. 그리고 학점별 비율이 나뉘는 평균 순위 30% 위치와 70% 위치의 점수가 기준점수 범위에 들어올 때까지 난이도별 배점을 조정한다. 이때의 기준점수는 평균과 표준편차를 지정한 정규분포표에서 추출한 100개 그룹의 시험점수를 기준으로 하였다. Fig. 3에서 100개 그룹의 시험점수 분석 결과에서 정한 기준점수를 설명한다.
Fig. 3의 데이터는 개인별 점수 0~100점 사이, 평균(mean) 67~73 사이, 표준편차(standard deviation) 8~14 사이로 지정한 정규분포표에서 개수(count) 35~40개 사이의 점수를 난수를 추출하여, 각 그룹별 최소값(min), 분위수(1%, 30%, 50%, 70%, 99%)값, 최대값(max)을 분석하였다. 그리고 100개 그룹의 분위수 30% 위치의 점수 평균과 표준편차를 계산했을 때, 평균은 63.77이고 표준편차는 2.19였다. 또한 분위수 70% 위치의 점수 평균과 표준편차를 계산했을 때, 평균은 76.08이고 표준편차는 2.86이었다. 같은 방법으로 100개 그룹의 데이터를 다시 추출하여 분석했을 때도 분위수 30%와 70% 위치의 평균과 표준편차는 크게 범위를 벗어나지 않음을 확인할 수 있었다. 이에 난이도별 배점을 재조정하는 데 이 점수를 기준점수로 하였다. 예를 들어 인원수 40명인 그룹에서 총점 순위 상위 12위의 점수가 76(±3), 상위 28위의 점수가 63(±3)이 될 때까지 난이도별 배점을 조정한다. Fig. 4는 전체적인 성적처리 알고리즘이다.
① 그룹의 시험 결과 데이터를 가져온다. ② 목표평균/최대배점/최소배점을 정한다. ③ 기준점수-1(상위 30%)과 기준점수-2(상위 70%) 값을 정한다. ④ 각 문항의 정답률을 계산한다. ⑤ 동일 배점을 기준으로 그룹평균(average-1)을 계산한다. ⑥ 정답률/그룹평균/목표평균을 이용하여 전체 문항의 난이도를 결정한다. ⑦ 난이도별 문항의 개수를 센다. ⑧ 그룹평균에 따라 시험 문항의 차등 배점 기준을 정한다. ⑨ 전체 100%의 비율에 맞추어 난이도별로 차등 배점을 정한다. ⑩ 차등 배점을 기준으로 그룹평균(average-2)를 계산한다. 그리고 상위 30%와 70% 위치의 점수가 기준점수 범위에 들어올 때까지 난이도별 배점을 조정한다.
4. 실험 결과 및 분석
A 대학에서 운영되는 교양 필수 과목인 프로그래밍 수업은 수강 인원 40명 이하로 여러 분반이 동시에 개설되며, 수업 내용 및 평가 등의 운영에 대한 기준은 정해져 있다. 동일 교수자가 여러 분반을 맡아서 수업을 진행하며, 각 교수자는 정해진 기준에서 크게 벗어나지 않는 범위에서 교수 재량으로 수업을 운영하고 분반별 상대평가 방식으로 학점을 부여한다. 평가 기준은 중간, 기말, 과제, 출석로 구성된다. 평가 기준에서 과제는 프로그램을 직접 작성할 수 있는가에 대한 실기 평가이다. 이는 평가 기간이 길고 다른 사람의 도움을 받아서 해결할 수 있는 영역이어서 학생별 점수 차이가 크지 않다. 최종 학점을 결정하는데 가장 큰 비중을 차지하는 중간시험과 기말시험은 시험 시간 50분 제한으로 수행되는 필기시험이며, CBT (Computer Based Test) 기반으로 이루어진다. 이는 사지선다형과 단답형으로 구성되며, 언어의 문법과 소스 분석 능력에 대한 평가이므로 학생들의 학습 능력에 따라서 점수가 다양하게 나타날 수 있다. A 대학에서는 중간시험과 기말시험이 끝나면 학생들의 점수를 개인별로 알려주어야 하며, 분반별 전체 성적 분포를 성적이 높은 순으로 정리하여 순위와 함께 공개해야 한다. 이에 학생들은 자신의 점수와 분반 안에서의 순위를 알 수 있으며, 이를 이용하여 자신이 받을 수 있는 학점의 범위를 대략 가늠해 볼 수 있다.
4.1 분반별 성적처리
본 논문에서 제시한 알고리즘을 성적처리에 적용했을 때, 각 분반의 그룹평균과 원점수 가지수 그리고 학점 비중이 나뉘는 구간의 점수를 비교 분석하였다. 성적처리는 파이썬 언어의 데이터분석 라이브러리인 Pandas를 이용하였다. Pandas 데이터 구조에서 DataFrame을 이용하여 성적처리를 수행하였다. 이때 describe 메서드의 percentiles 속성값을 이용하여 학생별 평균에 대한 상위 30%와 70% 위치의 구간 값이 기준점수 범위에 들어올 때까지 난이도별 차등 배점을 조정하였다. 그리고 Matplotlib 라이브러리를 이용하여 동일 배점을 적용했을 때와 본 논문의 알고리즘을 적용했을 때의 성적 분포를 그래프로 분석하였다.
Table 4에서 비교 분석한 평균은 수업을 직접 맡아 진행한 7개 그룹의 시험 결과이다. 동일 배점 기준을 적용한 시험 결과를 본 논문에서 제시한 알고리즘 기준으로 차등 배점 적용한 결과는 Table 5와 같다. 3.3에서 설명했듯이 모든 그룹에 대하여 같은 기준으로 같은 차등 배점을 적용한 (A)의 경우에는 동일 배점에 비해 그룹평균이 모두 낮아지는 현상이 발생했지만, 본 논문에서 제시한 알고리즘으로 차등 배점을 적용한 (B)의 경우에는 전체 7개 그룹의 그룹평균이 목표평균 70에 근접하고 있음을 알 수 있다. 이에 7개 그룹 중에서 목표평균에 가장 근접한 그룹-5와 학습 능력이 가장 높은 그룹-1, 학습 능력이 가장 낮은 그룹-7의 성적처리 결과를 자세하게 비교 분석한다.
4.2 목표평균에 가장 근접한 <그룹-5>
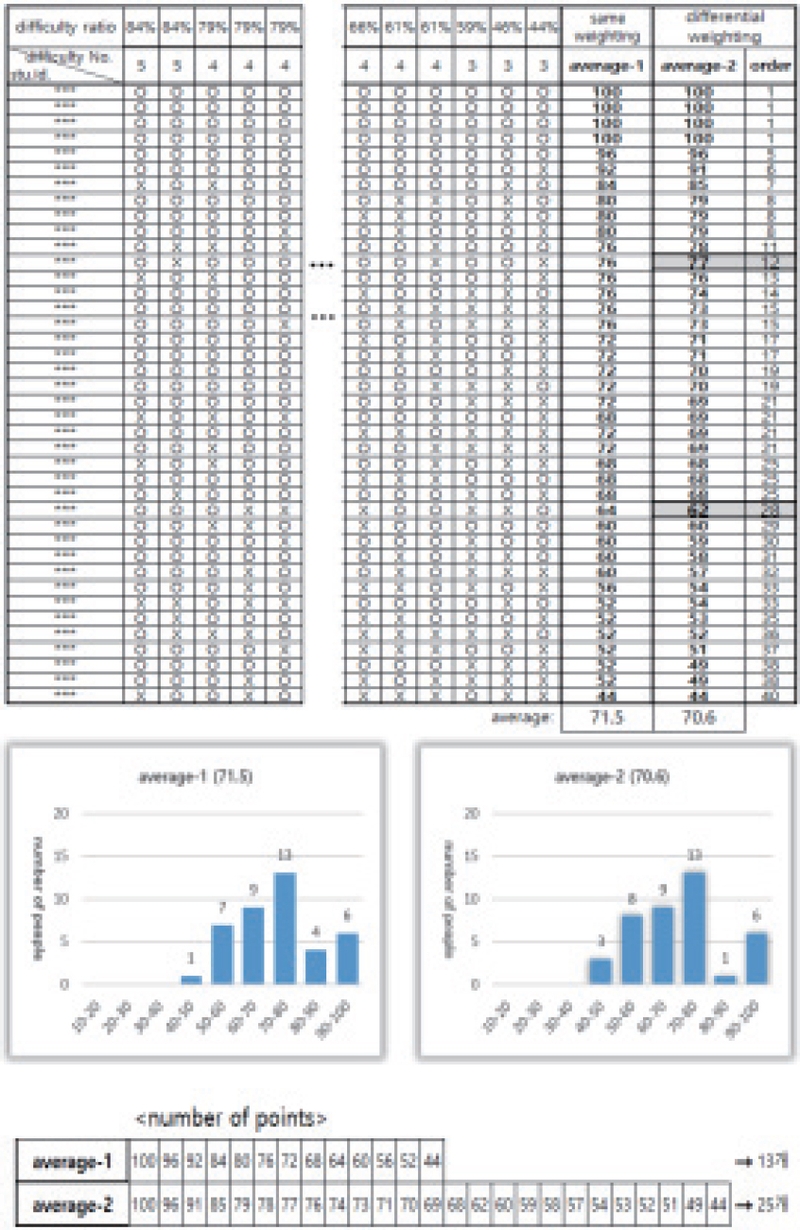
그룹-5는 동일 배점을 적용하여 그룹의 평균을 계산했을 때 71.5점으로 학습 능력이 교수자의 예측대로 목표평균에 가장 근접한 분반이다. 교수자의 판단을 배제하고 정답률 순위만으로 난이도를 상중(2개, 6점), 중(6개, 5점), 중하(10개, 4점), 하(7개, 2.5점)로 구분했을 때 그룹평균이 69.23이었다. 이에 본 논문에서 제시한 알고리즘을 적용했을 때의 난이도별 개수(number)와 난이도별 배점(weighting of item) 그리고 문항의 난이도 비율(ratio)은 최종적으로 Table 6과 같다.
먼저 동일 배점을 적용한 분반의 그룹평균(71.5)과 목표평균(70) 그리고 문항별 정답률을 기준으로 모든 문항의 난이도를 재조정한 결과, 난이도는 중(3개), 중하(20개), 하(2개)로 구분된다. 분반의 학습 능력으로 난이도를 재조정했을 때 대부분의 문항 난이도는'중하'에 해당함을 알 수 있다. 그룹평균이 목표평균 70점 이상이므로 난이도가 어려운 문항에 최대배점을, 난이도가 쉬운 문항에 최소배점을 지정하는 기준으로 전체 비율 100%에 맞추어서 중(5점), 중하(4점), 하(2.5점)를 적용하였다.
Fig. 5는 Table 6을 기준으로 성적 처리한 결과를 보인다. Fig. 5의 결과에서 average-1은 동일 배점을 적용했을 때의 그룹평균이고, average-2는 본 논문에서 제시한 알고리즘을 적용했을 때의 그룹평균이다. 두 경우의 그룹평균이 71.5와 70.6의 결과를 보인다. 그리고 학생별 평균에서 학점 비중이 나뉘는 구간인 상위 30% 위치(12위) 점수는 77점이고 70% 위치( 28위) 점수는 62점으로 모두 기준점수 범위에 포함되므로 더 이상의 배점 조정 없이 성적처리를 종료한다. 동점자 해소를 위한 학생들의 평균 점수 가지수(number of points)를 비교해 본 결과 average-1은 13개이며, average-2는 25개로 상대평가를 위한 충분한 가지수를 가지고 있음을 확인할 수 있다.
4.3 학습 능력이 가장 높은 <그룹-1>
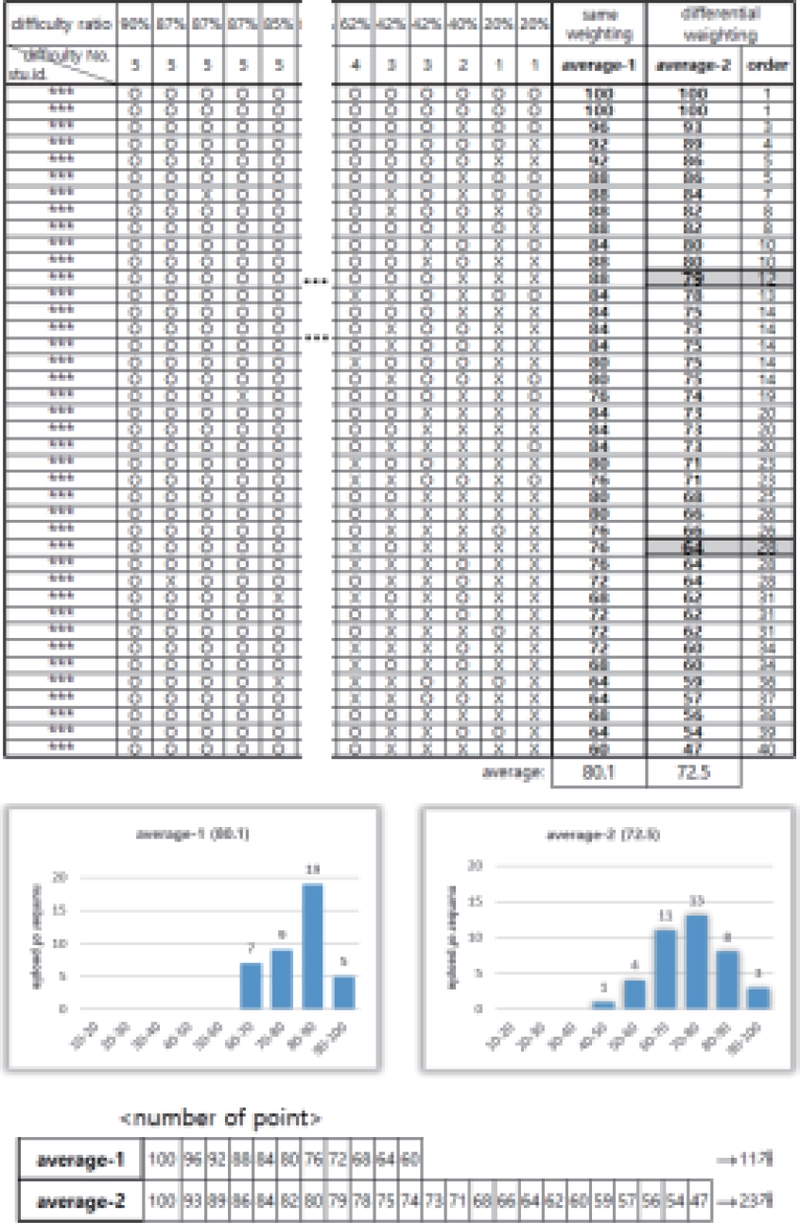
그룹-1은 동일 배점을 적용하여 그룹의 평균을 계산한 결과 80.1로 학습 능력이 가장 높은 분반이다. 교수자의 판단으로 출제된 문항이 분반의 학습 능력에 비해 쉬웠다는 의미이다. 정답률만으로 난이도를 상중(2개, 6점), 중(6개, 5점), 중하(10개, 4점), 하(7개, 2.5점)로 구분하여 같은 기준으로 차등 배점을 적용한 평균 점수는 76.45였다. 그리고 본 논문에서 제시한 알고리즘을 적용하여 문항의 난이도를 재조정한 결과, 최종 난이도별 개수(number), 난이도별 배점(weighting of item), 문항의 난이도 비율(ratio)은 Table 7과 같다.
학습 능력이 높은 분반에서 많이 틀린 문제는 난이도가 더 어려운 것으로 간주되어 '상'문제가 나타남을 알 수 있다. 분반의 평균이 목표평균 점수 70점에 근접하기 위해서는 전체 문제 비율에서 어려운 문제의 비율을 높여야 하기에 배점 기준을 난이도가 어려운 문항에 최대배점을, 난이도가 쉬운 문항에 최소배점을 지정하였다. 그리고 전체 비율 100%에 맞추어서 상(7점), 상중(6.5점), 중(5점), 중하(4점), 하(3점)로 정하였다. 그리고 평균 순위 상위 30% 위치와 70% 위치의 점수가 기준점수에 들어올 때까지 난이도별 배점을 재조정하였다. 그 결과 최종 난이도별 배점이 상(7점), 상중(6.8점), 중(6.5점), 중하(4.3점), 하(2.5점)에서 결정되었다. 성적처리 결과는 Fig. 6과 같다.
Fig. 6의 결과에서 본 논문의 알고리즘을 적용했을 때, 최종 평균이 72.5점으로 목표평균 점수 70점에 많이 근접해졌으며, 평균 순위 상위 12위의 점수는 79점, 28위의 점수는 64점으로 기준점수 범위에 포함됨을 알 수 있다. 또한 학생들의 평균 점수 가지수는 11개와 23개로 2배 정도의 차이를 보인다.
4.4 학습 능력이 가장 낮은 <그룹-7>
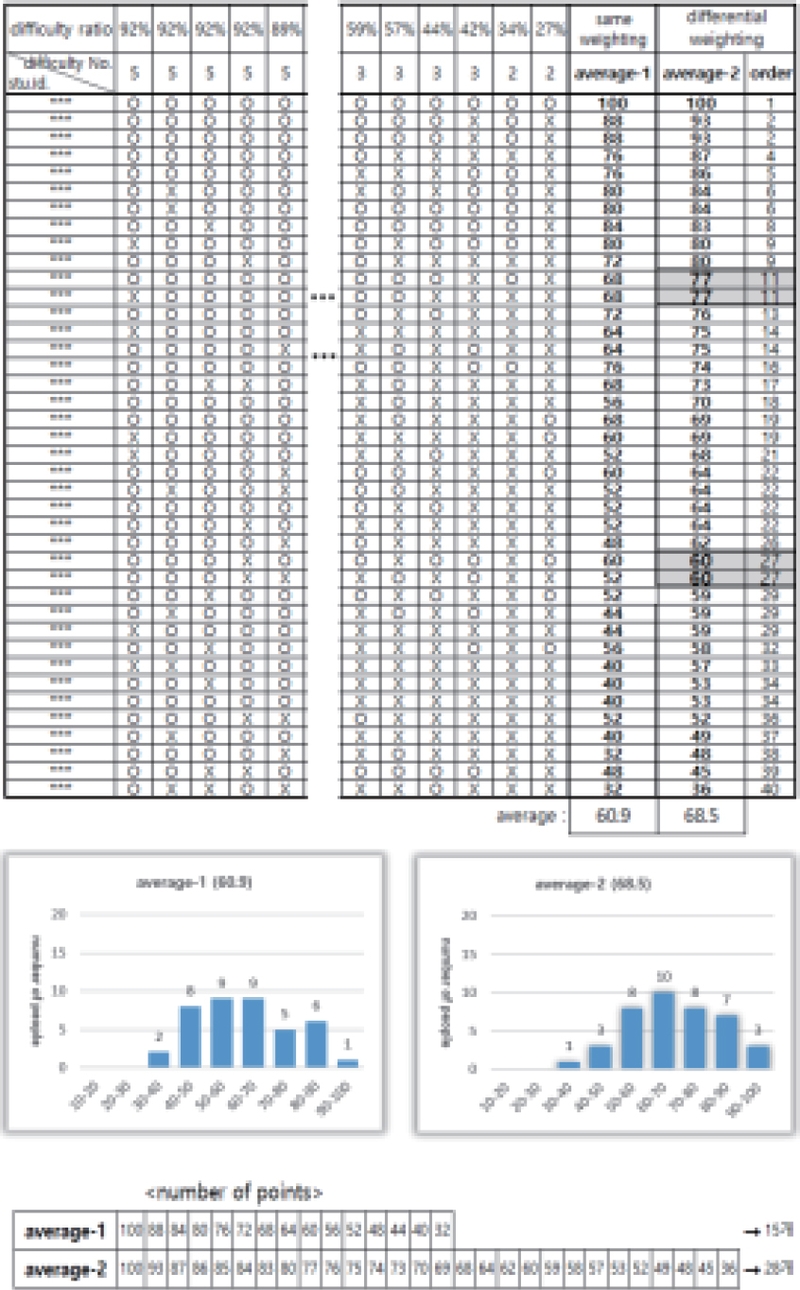
그룹-7은 동일 배점을 적용하여 그룹의 평균을 계산할 결과 60.9로 학습 능력이 가장 낮은 분반이다. 교수자의 판단으로 출제된 문항이 분반의 학습 능력에 비해 어려웠다는 의미이다. 정답률만으로 난이도를 상중(2개, 6점), 중(6개, 5점), 중하(10개, 4점), 하(7개, 2.5점)로 구분하여 같은 기준으로 차등 배점을 적용한 그룹평균은 56.20으로 목표 평균과의 차이가 더 벌어짐을 확인할 수 있다. 이에 본 논문에서 제시한 알고리즘을 적용하여 문항의 난이도를 재조정했을 때의 최종 난이도별 개수(number)와 난이도별 배점(weighting of item) 그리고 문항의 난이도 비율(ratio)은 Table 8과 같다.
학습 능력이 낮은 분반에서 많이 맞춘 문제는 난이도가 더 쉬운 문제로 간주되어 '하'문제가 늘어남을 보이고 있다. 분반의 평균이 목표평균에 근접하기 위해서는 전체 문항 비율에서 난이도가 쉬운 문항의 비율을 높이고 난이도가 높은 문항의 비율을 줄여야 한다. 이에 분반의 배점 기준을 난이도가 쉬운 문항에 최대배점을, 난이도가 높은 문항에 최소배점을 지정하여 전체 비율이 100%가 되도록 상중(2점), 중(2.4점), 중하(3점), 하(6점)로 정하였다. 그리고 평균 순위 상위 30% 위치와 70% 위치 점수가 기준점수에 포함될 때까지 난이도별 배점을 재조정하였다. 그 결과 최종 배점이 상중(2.2점), 중(2.3점), 중하(2.4점), 하(6.5점)에서 결정되었다. 성적처리 결과는 Fig. 7과 같다. 본 논문의 알고리즘을 적용했을 때, 최종 평균이 68.5점으로 목표평균 70점에 많이 근접해진 것을 확인할 수 있다. 또한 평균 순위 상위 30% 위치(11위, 2개) 점수가 77점이고, 70% 위치(27위, 2개) 점수가 60점으로 기준점수에 포함된다. 그리고 학생들의 점수 가지수도 15개와 28개로 거의 2배 차이가 남을 확인할 수 있다.
위의 결과에서 보이듯이 제시하는 알고리즘을 7개 그룹의 성적처리에 적용해 본 결과, 모든 분반의 그룹평균이 목표평균에 근접하고 학점 비중이 나뉘는 구간의 점수가 기준점수에서 크게 벗어나지 않는다는 것을 확인할 수 있었다.
5. 결론 및 향후 연구과제
대학에서 학업 성적을 평가하여 등급을 부여하면서 학점별 비율에 대한 규칙을 적용하는 강제배분 상대평가의 경우에는 평가 결과에서 얻은 점수의 집단 내 상대적인 위치가 학점의 중요한 변수로 작용한다. 특히 많은 수의 분반이 개설되는 교양 필수 과목의 경우에는 동일 교수자가 여러 분반을 맡아서 같은 학습 내용과 평가로 수업을 운영하고, 분반별 상대평가 방식으로 학점을 부여한다. 이때 분반이 서로 달라도 비슷한 평가 점수에 같은 등급을 부여하기 위해서는 각 분반의 그룹평균과 학점별 비율이 바뀌는 구간에서의 점수가 매우 중요하다고 할 수 있다. 이에 본 논문에서는 모든 분반의 그룹평균이 목표평균에 근접할 수 있도록, 그룹별로 학습 능력을 이용하여 시험 문항의 난이도를 재조정하고 문항의 차등 배점 기준을 달리 정하여 성적처리를 수행한다. 그리고 각 그룹에서 학점별 비율이 바뀌는 구간의 점수가 기준점수에 들어올 때까지 난이도별 차등 배점을 조정한다. 제시한 알고리즘을 성적처리에 적용하여 결과를 분석해 본 결과, 동일 배점과 기존의 차등 배점 알고리즘과 비교했을 때 모든 분반의 그룹평균이 목표평균에 근접하고 각 분반에서 학점별 비율이 바뀌는 구간의 점수 차이가 크지 않음을 확인할 수 있었다.
향후 연구과제로는 그룹의 학습 능력을 어떻게 판단할 것인지에 대한 보다 구체적이고 명확한 기준이 필요하다. 현재는 그룹평균 점수를 기준으로 그룹의 학습 능력을 평가하지만, 그룹 내에서 학습 능력이 높은 학생과 낮은 학생의 편차와 쏠림으로 인해 그룹평균 점수가 향상 혹은 감소하였을 때도 같은 방법으로 차등 배점 조정이 가능한지에 관한 추가적인 연구가 계속되어야 할 것이다.
References
-
Schleicher, D., Bull, R., & Green, S. (2009). Rater Reactions to Forced Distribution Rating Systems, Journal of Management, 35(4), 899-927.
[https://doi.org/10.1177/0149206307312514]

-
Goffin, R., Jelley, R., Powell, D., & Johnston, N. (2009). Taking advantage of social comparisons in performance appraisal: The relative percentile method, Human Resource Management, 48(2), 251-268.
[https://doi.org/10.1002/hrm.20278]

-
Berger, J., Harbring, C., & Sliwka, D. (2012). Performance appraisals and the impact of forced distribution - An experimental investigation, Management Science, 59(1), 54-68.
[https://doi.org/10.1287/mnsc.1120.1624]

-
Giumetti, G., Schroeder, A., & Switzer, F. (2015). Forced distribution rating systems: When does “rank and yank” lead to adverse impact?, Journal of Applied Psychology, 100(1), 180.
[https://doi.org/10.1037/a0037191]

-
Blume, B., Baldwin, T., & Rubin, R. (2009). Reactions to different types of forced distribution performance evaluation systems, Journal of Business and Psychology, 24(1), 77-91.
[https://doi.org/10.1007/s10869-009-9093-5]

-
Kim, Y., Kang, T., (2016). An exploratory study on the ability parameter estimation method considering the differential item weighing in multiple choice items, The Korean Journal of Educational Methodology Studies, 28(3), 521-538.
[https://doi.org/10.17927/tkjems.2016.28.3.521]

-
DeNisi, A., Wilson, M., & Biteman, J. (2014). Research and practice in HRM: A historical perspective, Human Resource Management Review, 24(3), 219-231.
[https://doi.org/10.1016/j.hrmr.2014.03.004]

- Yang, K. (2007). A study on the effectiveness of the Differential Item Weighting based on expert judgement, The Korea educational review, 13(1), 197-219.
-
Kim, J., Dong, H., Song, M., Nam, M., Kim, M., Choi, W., Lee, J., & Lee, E. (2010). An Analysis of the Determinants and the Validity of Item Weighting, The Journal of Curriculum and Evaluation, 13(2), 197-218.
[https://doi.org/10.29221/jce.2010.13.2.197]

- Ro, K., Park, C. (2001). An Information -based approach to compare items of different formats and different
- score points, Journal of Educational Evaluation, 14(2), 173-190.
-
Kim, K., Choi, E. (2002). Autumated Selection System of Examination Questions in Web-Based Instruction, KIPS Transactions on Computer and Communication Systems, 9(3), 301-310.
[https://doi.org/10.3745/KIPSTA.2002.9A.3.301]

-
Kim, E. (2019). A Study on Difficulty Equalization Algorithm for Multiple Choice P roblem in Programming Language Learning System, The Journal of Korean association of computer education, 22(3), 55-65.
[https://doi.org/10.32431/kace.2019.22.3.005]

Appendix
부 록

· 1996년 경상국립대학교 전자계산학과 (공학석사)
· 2001년 경상국립대학교 전자계산학과 (공학박사)
· 1990년 ~ 1993년 (주)LG전자 멀티미디어연구소 연구원
· 2001년 ~ 2003년 부산외국어대학교 전자컴퓨터공학부 전임강사
· 2003년 ~ 2005년 부산외국어대학교 교양학부 초빙교수
· 2008년 ~ 2010년 부산가톨릭대학교 컴퓨터공학과 전임강사
· 2019년 ~ 현재 국립부경대학교 교양교육원 강사
· 2023년 ~ 현재 부산교육대학교 대학원 창의IT융합 교육 강사
· 2010년 ~ 현재 부산대학교 교양교육원 강사
관심분야 : 프로그래밍 교육, 난이도 조정, 차등 배점
kimeunjung@pusan.ac.kr




![[그림 2] [그림 2]](/xml/45212/JKACE_2025_v28n5_19_apf001.jpg)
![[그림 3] [그림 3]](/xml/45212/JKACE_2025_v28n5_19_apf002.jpg)
![[그림 4] [그림 4]](/xml/45212/JKACE_2025_v28n5_19_apf003.jpg)
![[그림 5] [그림 5]](/xml/45212/JKACE_2025_v28n5_19_apf004.jpg)
![[그림 6] [그림 6]](/xml/45212/JKACE_2025_v28n5_19_apf005.jpg)
![[그림 7] [그림 7]](/xml/45212/JKACE_2025_v28n5_19_apf006.jpg)